Overview and Intended Learning Outcome

Quick Links

• Quick Links
• Announcements
• Syllabus and Schedule, Problem Sets, and Solutions
• Vital Information
• Textbook(s) and Lectures
• Policies and Grading

Announcements: see Canvas pages: Ph106b, Ph106c (accessible only to students registered for the course)

Syllabus and Schedule, Problem Sets, and Solutions

Below you will find the outline of Ph106bc.  I will update the details of the topics covered in lectures and suggested reading as the term progresses.  Assignments and exams will be made available via Canvas, about a week before the due date, so no effort is made here to list them.

The problem sets and solutions are only accessible via Canvas.  (Lecture notes are available to anyone.)

Keep a copy of the lecture notes and problem sets handy on your computer or a USB stick.  Websites go down occasionally (seemingly especially during holidays), and a very modest bit of foresight can prevent this from disrupting the problem set due date schedule.  If there is a problem set update, or a lecture notes update relevant to a problem set, at a very late date and there is an outage (in the 24 hrs before a set is due), this policy will be suspended.

In the suggested reading, G stands for Introduction to Electrodynamics by Griffiths, LN for Lecture Notes, HM stands for Classical Electromagnetism by Heald and Marion, and J for Classical Elecrodynamics by Jackson.  Reading given in parentheses is optional (intended only to tell you where material is drawn from).  The numbers in parentheses after each LN section listing and at the end of each day's lecture is the number of LN slides (to manage lecture pace).

Vital Information

Textbook(s) and Lectures

• Required: Introduction to Electrodynamics, Griffiths (4th edition!) available via the Caltech eCampus online textbook store.  (We are not going to adopt the 5th edition yet.)  No guarantees are made about whether the 3rd edition is sufficient for the course (though in the past it has been).
  
  
• Optional (all these will be available via the Course Reserves link in Canvas):
  

• Heald and Marion, Classical Electromagnetic Radiation
• Jackson, Classical Electrodynamics: the bible, but in general too advanced for this course.
  While this is not a required text, many students in past years have found it useful to buy it.  If you stay in physics, you will need it.  In addition to the hard copies, the library is able to make portions available electronically.  Those portions will be synchronized with the course.
  
• Landau and Lifshiftz, The Classical Theory of Fields
  
• Landau and Lifshiftz, Electrodynamics of Continuous Media

Other texts are included in the Course Reserves, but these are the most useful.

• Lecture Notes and Strategy:
  
  2024 version, updated 2024/06/07 06:30 with addition of all optional material, lectures 38 and 39 (no content changes to that material from 2023): pdf
  2023 final version: pdf
  
  My lecture notes generally follow Griffiths.  My goals in making them available to you are:
  
  • To provide clarification of points in Griffiths that I thought deserved more or alternate explanation.
    
  • To present additional explanation or material derived from other texts; the references will be provided in the notes and/or on the syllabus above.
  • To get all the calculational work down on the page, correctly, so that I don't have to do it in class.  In particular, text in magenta is calculational work that I skip over in class but which you are responsible.  If steps are unclear, ask the TAs or in the following lecture.
    
  
  I do not consider myself responsible for providing updated copies of the lecture notes well ahead of class time -- they are being updated as the course is being given.  The 2023 version of the notes is provided above and is frozen.  Change from 2023 will be minimal (aside from lecture breaks).  Updated notes will be posted promptly after class.
  

  Since the entire lecture notes are updated for every lecture, any annotations you make will be lost.  To keep them, I suggest that, after you annotate a section, you use "Extract Pages" in Acrobat and save that annotated section.
  

  The lecture notes may relieve you of the obligation of coming to lecture.  That's your choice.  Some students benefit from being able to receive information aurally and to interact during that process; others prefer to read it off the page.  I hope the interactive nature of the lectures will make them worth the time to attend.  But whatever works for you.  Grades are based only on the written work you submit.  
  
  But please do not delude yourself into thinking that, because the lecture notes are available, you can just skim through all the material for the week on the day before a problem set or exam is due and expect to immediately become expert.  Learning requires time to mull over concepts in your mind, for your subconscious to work on ideas and problems.  If you choose not to come to class, please be disciplined about keeping up with the material in your own study time.
  
  Back to the top.
  

Policies and Grading

The course will use the following policies on collaboration, honor code, assignment due dates and extensions, and credit:

• Homework is due 7 pm Fri via Canvas.
  
  
• Instructor or TA response to questions after 5 pm Friday should not be expected.
  
  
• Extension requests should be sent to me, the course instructor, not the TAs.  I do not check email continuously, and typically not after 5:30 pm on weeknights (until possibly after 8 pm), so your extension requests must allow time for non-immediate response.
  
  
• Extension requests must be based on conditions that could not be planned for or planned around: physical or mental health issue, family or other personal emergency, CASS accommodations, etc.  Other work (academic, research, other), extracurricular activities, etc. that were known about ahead of time and could be planned for are generally not considered acceptable reasons, though in some cases they can be.  The deans have reiterated this policy to instructors, with the goal of ensuring students do not have work piled up at the end of term due to extensions earlier in the term.  Do the best you can and turn in what you have if you did more than half the problem set, otherwise take the 50% credit extension and turn in the work a week late.
  
  If you have a CASS accommodation, please note it in your extension request.
  
  
• Late work policy
  • You may turn any problem set up to 1 week late for 50% credit.  Splitting of sets is not allowed: Turn in what you have on time for 100% credit, or turn in more or all of the set late for 50% credit, but you may not do both.
  • You may have one silver bullet extension each for Ph106b and one for Ph106c.  A silver bullet provides a 1-week extension at full credit.  It does not push out the due date, so one cannot take an additional 1-week extension at 50% credit; it is a replacement of the 50% credit period by 100% credit.
  You do not need to request permission ahead of time for the above, just note it at the top of the submitted problem set.  Let us know if late work is occurring near the end of term so we don't miss giving credit for the work.
  
  
• The grading split will be
• 50% problem sets
• 25% midterm exam
• 25% final exam
  
  
• Extra credit for problem session attendance: To encourage attendance at the Monday problem sessions, we will offer extra credit.  Here are the rules on the extra credit:
• The extra credit will be added after the letter grade boundaries are decided, so students who do not attend will not be penalized.
  
• Students who miss no more than one problem session in Ph106b or Ph106c (separately for the two courses) will be guaranteed one +/- grade increment of extra credit.  Students who attend fewer sessions will receive a proportional point increment.  The latter may or may not result in a +/- grade increment depending on the details of the person's numerical grade.
• Extra credit does not apply to the A/A+ boundary: A+ grades must be earned on the basis of submitted work.
  
• If you have a time conflict with the problem session time, contact the course instructor to identify an alternate solution.
  
  
• Honor code and Collaboration policy
  
  
• Use of mathematical software like Mathematica is allowed on homework, but will not be available for exams.  From a former colleague: It is absolutely essential that you develop a strong intuition for basic calculations involving linear algebra, differential equations, and the like.  The only way to develop this intuition is by working lots of problems by hand; skipping this phase of your education is a really bad idea.
  
  
• HOMEWORK COLLABORATION AND REFERENCE POLICY
  
  You must first try the problems yourself.  If you get stuck, or are unsure of your answer, you may seek help from the TAs or the instructor (see office hours above). You may also seek help from other students in the course, but your solution must be the result your own understanding of the material and must be written up independently (e.g. not copied from someone else's solutions or from a jointly prepared solution). If you do work with other students on a problem set, you must identify the names of those with whom you worked with on the submitted work.  Don't let your colleagues show you how to do the problems; make sure they are helping you by "Socratic Method" -- asking you questions that will lead you to the insight you need for a particular problem.
  
  It is probably possible to find the solution to any reasonable problem in other textbooks, from previous years of Ph106, or on the internet. You must not seek solutions to the assigned problems from any such resource. In any case, this would be a foolish thing to do, since the assignments serve as practice for the midterm and final for which consulting outside sources is not allowed. You should also not consult others who have taken Ph106 in a previous year for copies of the problem sets, but of course you may request help as you would from a TA.
  
  Historically, performance on problem sets is much better than on exams (see below).  Some of this may be due to the exam time constraint, but some of it may also be due to problem set overcollaboration.  If you do not internalize the material via the problem sets, you will not do well on the exams.  So be very careful to follow the collaboration policies, not just because of the honor code, but for your own good.
  
  Here are some elaborations on the collaboration and reference policies, intended to supplement, not replace, the above policies:
  
  
  • On consulting tutors, TAs, fellow students, etc:
    
    Remember what the collaboration policy says: you must first try the problems yourself.  You can consult the instructor, TAs, tutors, fellow students, etc., but your solution must be the result of your own understanding.  You cannot ask other people to show you how to do a homework problem, or watch them do it, only discuss general issues and concepts with them, or work different examples.
    
    Generally, homework problems appear difficult because either the underlying physics or the calculational technique has not been understood.  Understand those and the homework is doable on your own.
    
    
  • On assisting fellow students:
    
    The same rules apply.  Don't tell your fellow students how to do a problem.  You can help them figure it out themselves by discussing relevant concepts, other examples, etc.  Helping another student without explicitly showing them how to do a problem is helpful to your own understanding, also, as you must have the concepts and techniques clear in your own head in order to effectively explain them to another student.  Use the "Socratic Method" -- ask questions that will lead your colleague to the insight needed to figure out the problem on their own.
    
    
• EXAM COLLABORATION AND REFERENCE POLICY
  
  Exams are strictly non-collaborative!
  
  Exams are "open-book": You may consult your own notes (both in-class and any additional notes you take), Griffiths, and handouts and solution sets on this website.  No other textbooks (not even Jackson and Heald & Marion, since they are optional), no web sites, no other resources.
  
  In some instances, you may make use of notes taken from online resources. In particular, if you take the initiative to study beyond class material and you get lucky by finding or studying ahead of time a problem that is later assigned on homework or an exam, you get to benefit from your hard work. However, you may not go hunting for problems on the web after they have been assigned, and you must use your own notes (handwritten or electronic) on any materials you have found, not the original source material.
  
  The most extreme hypothetical is the case of finding on the web a problem that is assigned on homework or an exam.  If you find the problem before seeing the relevant homework or exam, and take notes on it in your own hand (real or virtual), then those notes are fair game for use while you are doing the homework or exam. If you see the homework or exam, then go searching on the web and find the problem, your notes on such a problem are not allowed. Even if you found the problem before you saw the exam and saved the solution on your computer, going back to that saved copy is also not allowed, since that would not be your own notes.
  
  While it follows the letter of the above policy, hunting down scores of problems ahead of time and copying them in one's own hand is strongly discouraged. Doing so clearly violates the spirit of the law, and the large amount of time it takes to find and copy these solutions could be much better spent learning the material.
  
  If you do make use of electronic resources and save them, one idea would be to create a "forbidden" folder on your computer that you know you may not consult during an exam.  This will prevent even accidental violations of the honor code.
  
  
• You may use the previous years' exams and solutions posted on the Canvas website when doing problem sets or exams, but only those!  You may not use previous years' exams or solutions that are not available from this website or the Canvas website.
  
  
• You may use any other materials provided by the instructor or TAs, including material from the problem sessions or office hours.
  
  
• AI/ONLINE TUTORING POLICY
  
  This course will adhere to the PMA policy on the use of AI and online tutoring.  The portions of that policy relevant to this course are as follows (and are consistent with what is stated above about use of internet resources):
  
  A primary goal of education is to learn how to approach and how to think about problems. Rapidly evolving generative artificial intelligence tools (e.g. ChatGPT, Bard, etc), online tutoring services (e.g. Chegg) and internet resources (e.g. Google) have the potential to be powerful companions for learning. On the other hand, they also provide tempting shortcuts to solutions that can be seriously detrimental to student learning. The course policies below serve to ensure that artificial intelligence (AI), internet resources (IR) and online tutoring (OT) usage in our class is carried out responsibly and ethically.
  
  Permissible Uses of AI, IR & OT
  
  Augmenting learning: AI, IR & OT can be used as a virtual TA to help clarify concepts learned in class, to provide example problems/solutions that supplement course material, and to inquire about advanced topics beyond the scope of the course.
  
  Prohibited Uses of AI, IR & OT
  
  Generating solutions: Unless explicitly allowed by the instructor, AI, IR & OT cannot be used to generate answers to any class assignment (e.g. problem sets, quizzes, exams), even if the student revises or recreates the content with the exception of the scenario described above. If there is any confusion about AI, IR & OT policy, the student should seek clarification before using them for any assignment.
  
  Guidelines for Using AI, IR & OT in Permissible Cases
  
  Understanding and Learning: Students may use AI, IR & OT to enhance their learning. However, these should not replace primary methods of learning, such as attending lectures, reading assigned textbooks, participating in sections and office hours, and practicing independent problem-solving. Students should take advantage of the unique opportunities associated with being enrolled in-person at Caltech.
  
  Critical thinking: Students should note that material generated by AI, IR & OT may be inaccurate, incomplete, or otherwise problematic. Students should ensure they are learning from reliable sources. Beware that over-reliance on these tools may also stunt the development of independent thinking and creativity. 
  
  Consequences of Violating the AI, IR & OT Use Policy
  
  Any student who violates the AI, IR & OT use policy is subject to the same disciplinary actions as for a Caltech Honor Code violation.
  

• Ditch day policy (Ph106c): 
  

• If ditch day falls on a lecture day, I will reschedule the lecture for the Saturday following ditch day, probably at 2:00 pm.  If ditch day falls on a problem set due day or the day before (Thursday or Friday), the set due date will be delayed to the following Monday, usual time.  If that Monday is a holiday, then the set will be due Tuesday at the usual time.
  
  
• A delayed problem set due date due to ditch day has no impact on later problem set due dates, including 50% credit and silver bullet extensions.  If ditch day falls just before a holiday weekend, pushing the due date to Tuesday, there is the prospect of a very short following week to do the next set.  Plan accordingly by starting the next set over the weekend while finishing the set that was due during the week of ditch day.
  
  
• Office Hours: 
  
• If ditch day falls on a Thursday, Thursday and Friday office hours will be rescheduled for Saturday/Sunday.  
  
• If ditch day falls on a Friday, then causality requires that we not change the Thursday office hour schedule.
• If Monday is a holiday, shift the above by one day, availability permitting.  
  
• So, for those of you who might be making decisions on acausal information, take account of the above information.

Grade Distributions

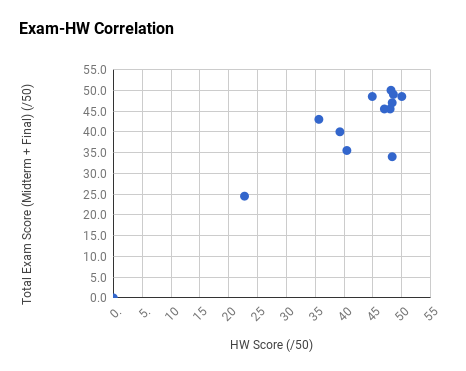
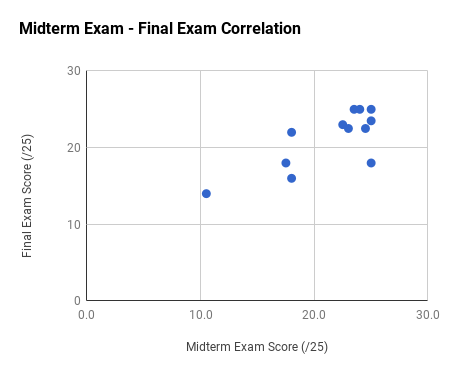
Note the very strong final exam vs. midterm exam correlation and the weak total exam vs. homework correlation.  Too much collaboration on homework can leave one unprepared for the non-collaborative exams.

Ph106b (2024; note that all histograms are before extra credit):

Ph106c (2024; note that all histograms are before extra credit):





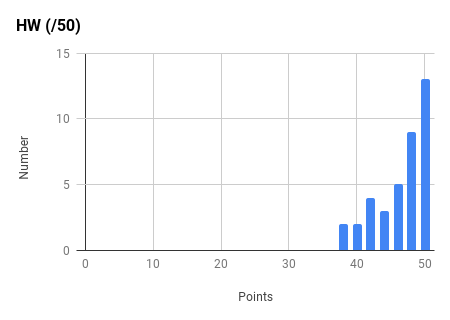
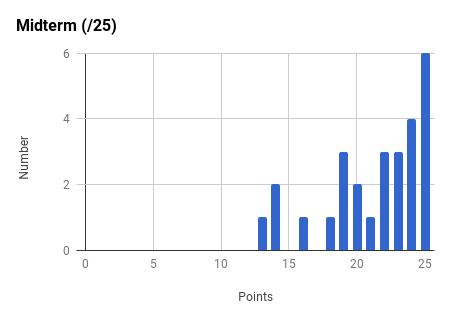
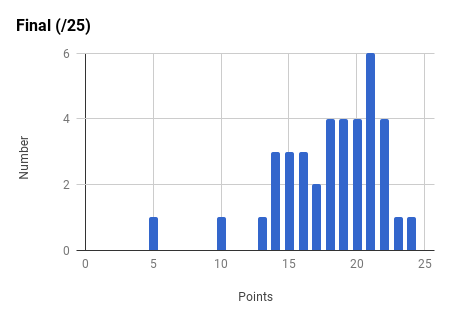
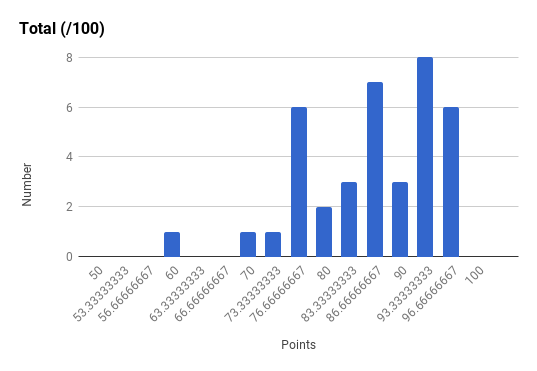
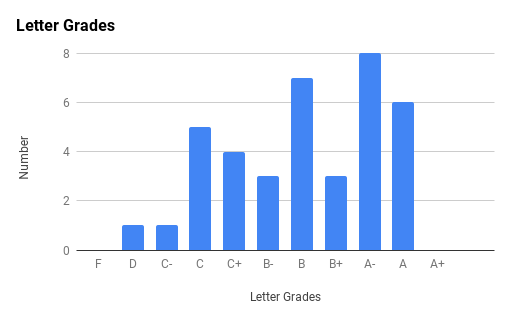
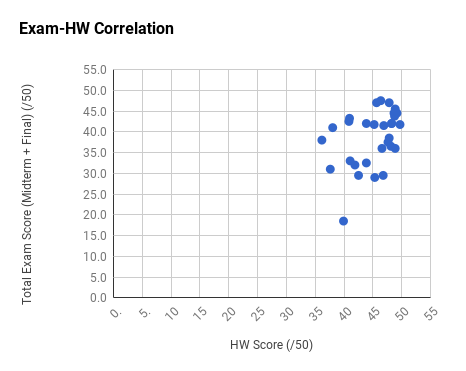
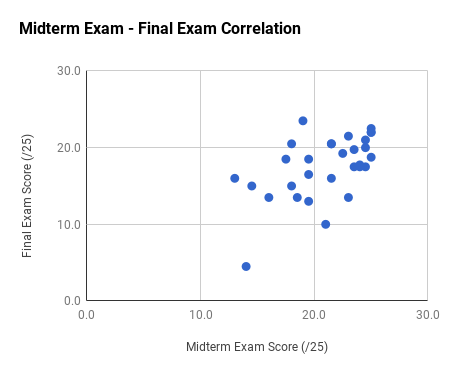
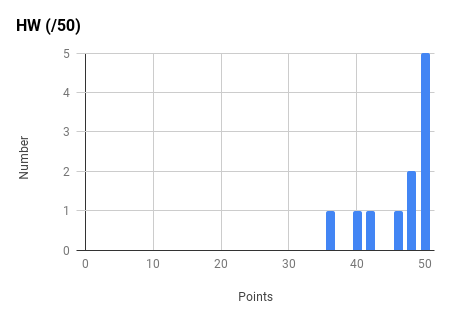
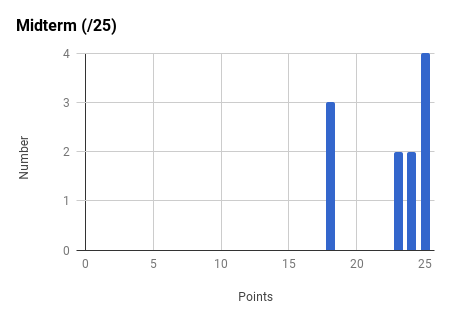
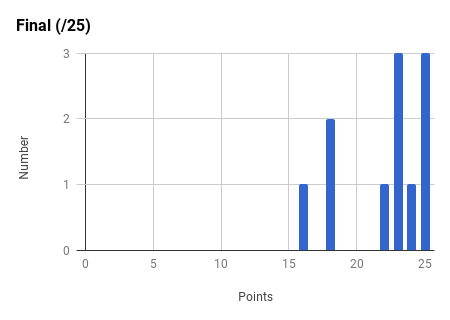
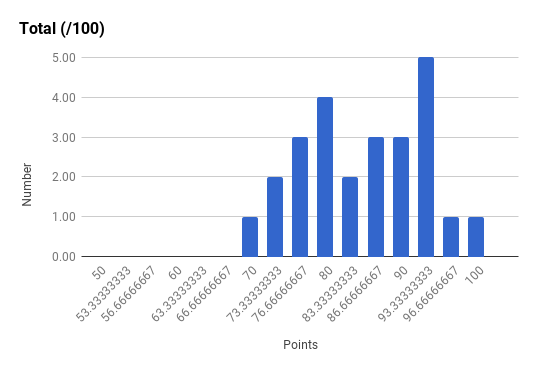
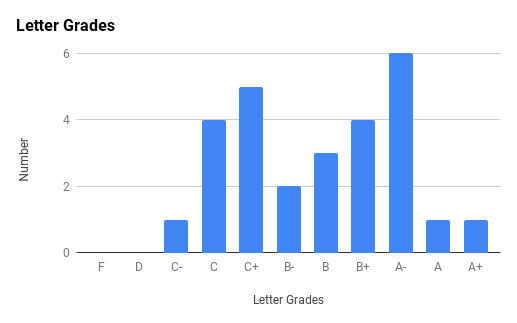
Back to the top.