Physics 106ab
Fall Quarter, 2006 and Winter Quarter, 2007
Course Homepage
Overview
The Ph106abc sequence covers classical
mechanics and electromagnetism
at a level of sophistication beyond the introductory Ph1/2/12
sequence. You will learn a variety of new techniques and
formalism that will allow you to attack a wider set of problems than
you saw in the introductory sequences as well as provide you a deeper,
more unified understanding of the structure and fundamental principles
of classical physics. Ph106a and the first half of Ph106b will
cover classical mechanics and special relativity. The remainder
of Ph106b and all of Ph106c will cover classical electromagnetism.
This is the home page for the classical mechanics/special relativity section of Ph106ab.
The classical electromagnetism half of Ph106bc will be taught by Prof. Cross.
This is the home page for the classical mechanics/special relativity section of Ph106ab.
The classical electromagnetism half of Ph106bc will be taught by Prof. Cross.
Quick Links
- Announcements
- Vital Information
- Textbook(s)
- Lecture Strategy
- Problem Set Policies
- Grading
- Syllabus and Schedule, Lecture Note References, Problem Sets, and Solutions
- Exams
- Practice Problems
Announcements
- 2007/03/29
- Updated grade histograms and anonymous grade sheets posted below, including all grades for
winter term. Please check for clerical errors!
- 2007/03/02
- Updated grade histograms and anonymous grade sheets posted (include EM sets) -- see below. Check for clerical errors!
- We have corrected grades on many Midterm Problem 3's by now;
the exam median has gone up to 59!
Vital Information
Location:
107 Downs
Time: TuTh 10:30 am - 12:00 pm
Instructor: Prof. Sunil Golwala, 311 Downs, Mail Code 59-33, golwala at caltech.edu
Teaching Assistants:
Time: TuTh 10:30 am - 12:00 pm
Instructor: Prof. Sunil Golwala, 311 Downs, Mail Code 59-33, golwala at caltech.edu
Teaching Assistants:
Andrey Rodionov, rodionov at caltech.edu
Peng Wang, pengw at its.caltech.edu
Please contact the TAs directly if you would like to make appointments outside of normal office hours.
Office Hours and Contact Information:Peng Wang, pengw at its.caltech.edu
Please contact the TAs directly if you would like to make appointments outside of normal office hours.
Prof. Golwala: 9:00
pm-11:00 pm Thursdays, 311 Downs (may move to 107 Downs if attendance
is high). Additional
office hours by
appointment or by popular
demand. If
you need to contact me outside of office hours, please try email
first. I am happy to arrange meetings outside of normal
office
hours, but I am not always available on the spur of the moment.
Please
include "Ph106" in the subject line of your email -- I get a
lot of email, and I want to make sure I see your emails quickly.
TAs:
Wednesdays, 9:00 pm - 11:00 pm Sherman Fairchild Library Room 231, on the 2nd floor
The TAs will alternate on the Wednesday office hours.
Wednesdays, 9:00 pm - 11:00 pm Sherman Fairchild Library Room 231, on the 2nd floor
The TAs will alternate on the Wednesday office hours.
Feedback:
I greatly appreciate student
feedback; feedback prior to the end-of-term evaluations lets me modify
the class to fit your needs. In
person, by email, by campus mail, whatever you like. If you would
like
to preserve your anonymity, campus mail will usually work. I have
mailboxes on the 3rd floor of Downs near my office and in 61 W.
Bridge.
Ombudspersons: I would also like to have two student ombudspersons for the class. Contact me to volunteer.
Ombudspersons: I would also like to have two student ombudspersons for the class. Contact me to volunteer.
Textbook(s)
- Required: Analytical Mechanics,
Hand and Finch, available at the bookstore.
- Suggested: Classical Dynamics of
Particles and Systems, Thornton (2004), textbook and student
solutions manual, available at the bookstore.
This text is somewhat less advanced than Hand and Finch, but has the significant benefit of having many more examples and problems as well as a student solutions manual for roughly one-third of the problems. If you find yourself unhappy with the presentation in Hand and Finch or wanting more examples and problems, you should buy this book. Thornton does not, however, cover everything in H&F; there is no discussion of virtual work, canonical transformations, or action-angle variables. The treatment of special relativity is somewhat elementary.
- Optional (on 3-hr reserve
at Fairchild Library):
Use these optional texts for alternate explanations or for additional problems or examples. The basic material is always the same, but different authors have different approaches. The break point between "intermediate" and "advanced" texts is usually the degree of attention they pay to the more formal aspects of classical mechanics, especially Hamilton-Jacobi theory. Modern texts such as Jose also take a very geometric point of view, which is elegant but can be too much the first time around.
- Intermediate: just below or at the level of this course
- Analytical Mechanics, Fowles and Cassiday (1999)
- Mechanics, Symon
(1971)
- Advanced: at or above the level of this course
- Classical Dynamics,
Jose (1998)
- Classical Mechanics,
Goldstein (2002)
- Mechanics, Landau
and Lifshitz (1976)
- Lecture Notes:
My lecture notes in general follow Hand and Finch and are primarily intended as a distillation for my personal use. It will appear in class that I am working directly from them because I am -- that's why they're called lecture notes! They will in general provide clarification of points in H&F that I thought deserved more or alternate explanation. Occasionally they may contain additional explanation or material derived from other texts; the references will be provided in the notes.
Bound copies of my lecture notes are available from the bookstore. Electronic versions are available here:
- 2006/09/25 version of notes, matches bookstore version: pdf.
- Errata in 2006/09/25 version: pdf (updated 2007/01/15)
- Up-to-date version of lecture notes including all errata
listed above (updated 2007/01/15): pdf.
Lecture Strategy and
In-Class Problems
I will not cover in lecture every bit
of material
you will be responsible for. There are some topics that are
really better covered by reading than by lecture, and some topics that
are simple enough that they are a waste of lecture time. I can
use the leftover time to do more examples.
Problem Set Policies
The best way to learn physics is by
doing problems. In addition to the regular problem sets, Thornton
has many problems with full solutions in the Student Solutions
companion volume. Below, I also provide last year's problem sets;
solutions are available upon request.
- Problem sets will be posted below,
linked
to the syllabus, usually on the Friday or Saturday 1
week before they are due.
- Due date: Fridays by 5
pm, at my office (311 Downs). 5
pm means 5 pm. No mercy will be granted. Remember,
we give partial credit, so the last 10 minutes of work will not make
much difference.
- Late policy: Problem sets will be accepted up to 1 week late (5
pm the following Friday) for
50% credit, and after that not
at all. You may turn in part on-time and part late. Please note on the problem set if it is
being split this way. You do not need to contact me or
the TAs
to turn in a problem set late at 50% credit, or to turn in part on-time
and part late.
- Extensions:
- You may take one
full-credit one-week extension per term. No need to contact us,
just write it on your problem set.
- Otherwise, extensions will be granted for good
reasons -- physical or mental health issues, family emergency,
etc. You must contact me or one of
the TAs before the homework is
due and you must provide some sort of proof (e.g., note from resident
head, health center, counseling center, or Barbara Green). A
heavy amount of other
coursework is not
sufficient reason for an extension (though you may use your free
extension in such circumstances -- so save it until you really need
it!).
- Solution sets will be posted in the
same location when the homework
sets are
due (usually Friday night or
Saturday morning). If you turn in the problem set late, you may not look at the
solutions until you have turned in your problem set.
- Graded problem sets will be available
roughly 10 days after they are
due, outside my office.
Grading
The course grade will be one-third
homework
sets, one-third midterm, and one-third final.
Collaboration is permitted on homework sets, but each student's solution must be the result of his or her own understanding of the material. No manual xeroxing is allowed. See below for some comments on working in groups.
Use of mathematical software like Mathematica is allowed, but will not be available for exams. Prof. Mabuchi makes a very good point on his Ph125 web site: It is absolutely essential that you develop a strong intuition for basic calculations involving linear algebra, differential equations, and the like. The only way to develop this intuition is by working lots of problems by hand; skipping this phase of your education is a really bad idea. Be careful how you use such packages.
The midterm and final are not collaborative, though you are welcome to consult your own notes (both in-class and any additional notes you take), Hand and Finch, and my lecture notes (including typo corrections). Thornton is not allowed because it is not a required text. You may not use other textbooks, the web, any other resources, or any software of any kind.
Ph106/196 option:
For Ph106a, we are going to offer an alternate registration option, Ph196a. Ph196a students will attend the same lecture as Ph106a students, but will be assigned extra reading material covering advanced topics (which will not be covered in lecture), will be assigned more difficult problems for homework sets and exams, and will be graded more rigorously. This option is being provided to address the wide range of readiness and ability in students taking Ph106a; in past years, we had a very large spread, making it difficult to provide a course that met everyone's needs.
I emphasize that there is no disgrace in taking the 106a option. You have had only 1 quarter of mechanics by this point in your undergrad education, and expecting everyone to get up to speed on all the subtleties of analytical mechanics in one term is simply unreasonable. A 106a-level class is typical of most universities. The class I took as an undergrad was much more like 106a than 196a; I don't think I would have been ready for 196a.
If you just want to register for Ph196a, simply complete an add/drop form as if you were doing a standard class drop and add. It is possible to register for Ph196a now and drop into 106a later if you are not happy with your performance. Dean Hall says that you should sign up for Ph196a initially. If you later want to drop down to Ph106a, it will be treated as a section change. You will have until drop day to do this. You should not attempt to register for both courses, so you will not need to worry about making an overload petition. Note that we will use your Ph196a problem set and exam grades up to the point at which you switch, so there is a risk in starting in Ph196a.
This policy is being continued into winter term as Ph106b/Ph196b. Whether it continues to spring term will be decided by Prof. Cross.
Grade Distributions and Anonymously Listed Grades
Collaboration is permitted on homework sets, but each student's solution must be the result of his or her own understanding of the material. No manual xeroxing is allowed. See below for some comments on working in groups.
Use of mathematical software like Mathematica is allowed, but will not be available for exams. Prof. Mabuchi makes a very good point on his Ph125 web site: It is absolutely essential that you develop a strong intuition for basic calculations involving linear algebra, differential equations, and the like. The only way to develop this intuition is by working lots of problems by hand; skipping this phase of your education is a really bad idea. Be careful how you use such packages.
The midterm and final are not collaborative, though you are welcome to consult your own notes (both in-class and any additional notes you take), Hand and Finch, and my lecture notes (including typo corrections). Thornton is not allowed because it is not a required text. You may not use other textbooks, the web, any other resources, or any software of any kind.
Ph106/196 option:
For Ph106a, we are going to offer an alternate registration option, Ph196a. Ph196a students will attend the same lecture as Ph106a students, but will be assigned extra reading material covering advanced topics (which will not be covered in lecture), will be assigned more difficult problems for homework sets and exams, and will be graded more rigorously. This option is being provided to address the wide range of readiness and ability in students taking Ph106a; in past years, we had a very large spread, making it difficult to provide a course that met everyone's needs.
I emphasize that there is no disgrace in taking the 106a option. You have had only 1 quarter of mechanics by this point in your undergrad education, and expecting everyone to get up to speed on all the subtleties of analytical mechanics in one term is simply unreasonable. A 106a-level class is typical of most universities. The class I took as an undergrad was much more like 106a than 196a; I don't think I would have been ready for 196a.
If you just want to register for Ph196a, simply complete an add/drop form as if you were doing a standard class drop and add. It is possible to register for Ph196a now and drop into 106a later if you are not happy with your performance. Dean Hall says that you should sign up for Ph196a initially. If you later want to drop down to Ph106a, it will be treated as a section change. You will have until drop day to do this. You should not attempt to register for both courses, so you will not need to worry about making an overload petition. Note that we will use your Ph196a problem set and exam grades up to the point at which you switch, so there is a risk in starting in Ph196a.
This policy is being continued into winter term as Ph106b/Ph196b. Whether it continues to spring term will be decided by Prof. Cross.
Grade Distributions and Anonymously Listed Grades
Syllabus and Schedule, Lecture Note References, Problem Sets, and Solutions
Boldface:
major topic for day
Normal typeface: specific topics to be covered.
Italicized typeface: Ph196 topics; Ph106 students will not be responsible for italicized topics.
LN = Lecture Notes
HF = Hand and Finch
Th = Thornton (Thornton reading always optional)
Normal typeface: specific topics to be covered.
Italicized typeface: Ph196 topics; Ph106 students will not be responsible for italicized topics.
LN = Lecture Notes
HF = Hand and Finch
Th = Thornton (Thornton reading always optional)
| Tuesday
Class |
Thursday
Class |
Friday Problem
Set |
| Fall, 2006 |
||
| Sep 26 review of Newtonian mechanics LN 1.1.1-1.1.2 (Th 2.1-2.5) |
Sep 28 review of Newtonian mechanics gravitation LN 1.1.3 and 1.2 (Thornton Ch. 2.6, 5) |
Sep 29 Problem Set 1 posted v. 2 posted 10/1 |
| Oct 3 dynamics of systems of particles LN 1.3.1 generic results (Th. 9.1-9.5) |
Oct 5 dynamics of systems of particles virial theorem collisions LN 1.3.2 (Th 9.6-9.8) |
Oct 6 Problem Set 1 due solutions posted (v. 2!) Problem Set 2 posted |
| Oct 10 fundamentals of Lagrangian mechanics constraints and generalized coords nonholonomic constraints virtual work generalized equation of motion LN 2.1.1-2.1.3 HF 1.1-1.7 |
Oct 12 applications of Lagrangian mechanics conservative forces and Lagrangians Euler-Lagrange equations solving problems with E-L eqns LN 2.1.4-2.1.8 HF 1.8-1.11 |
Oct 13 Problem Set 2 due solutions posted Problem Set 3 posted v. 2 posted 10/15 |
| Oct 17 special topics in Lagrangian mechanics Lagrangians for nonconservative forces symmetry transformations Noether's theorem LN 2.1.9-2.1.10 HF 1.11-1.13, 5.1-5.2 (Th 7.9) |
Oct 19 variational dynamics, incl. constraints calculus of variations principle of least action and E-L eqns Lagrange multipliers for holonomic constraints LN 2.2.1-2.2.3 HF 2.1-2.7 (Th 6.1-6.5, 7.1-7.7) |
Oct 20 Problem Set 3 due solutions posted Problem Set 4 posted v. 2 posted 10/25 |
| Oct 24 constraints in variational dynamics Examples using Lagrange multipliers Variational techniques for nonholonomic constraints LN 2.2.3-2.2.4 HF 2.6-2.8 (Th 6.6, 7.5) Hamiltonian dynamics Legendre transformations Hamiltonian dynamics -- theory Hamiltonian dynamics -- examples LN 2.3.1 HF 5.3-5.5 (Th 7.10-7.11) |
Oct 26 advanced topics in Hamiltonian dynamics phase space Liouville's theorem Virial theorem LN 2.3.2, 2.4.1 HF 5.6, 6.1-6.2 (Th 7.12) |
Oct 27 Problem Set 4 due solutions posted v. 2 posted 11/10 Midterm posted |
| Oct 30 advanced topics in Hamiltonian dynamics canonical transformations symplectic notation Poisson brackets generating functions action-angle variables and adiabatic invariance via generating functions LN 2.4.2-2.4.4 HF 6.3, 6.5 |
Nov 2 advanced topics in Hamiltonian dynamics Hamilton-Jacobi theory and examples LN 2.4.5 HF 6.5 |
Nov 3 Midterm due solutions posted (v. 2 posted 2006/11/07) Problem Set 5 posted |
| Nov 7 action-angle variables adiabatic invariants simple harmonic oscillators simple harmonic oscillator damped and driven SHO Green's functions for SHO LN 3.1.1-3.1.4 HF 3.1-3.7 (Th 3.1-3.5, 3.7-3.9) |
Nov 9 simple and coupled harmonic oscillators Green's functions for SHO SHO resonance phenomena finding normal modes LN 3.1.5, 3.2.1-3.2.2 HF 3.8-3.9, 9.1-9.3 (Th 3.6, 12.1-12.4) |
Nov 10 Problem Set 5 due solutions posted solutions updated 12/3 Problem Set 6 posted v. 2 posted 11/16 |
| Nov 14 No lecture (observing galaxy clusters, watching the virial theorem in action) |
Nov 16 coupled oscillations applying initial conditions mathematical structure degenerate modes loaded string continuous string LN 3.2.2-3.2.4, 3.3.1-3.3.3 HF 9.4-9.7 (Th 12.5-12.9, 13.1-13.?) |
Nov 18 Problem Set 6 due solutions posted solutions updated 12/4 Problem Set 7 posted NOTE: PS7 is LONG You have 2 weeks for it. Plan accordingly! |
| Nov 21 central force motion assumptions effective 1-D eqn of motion qualitative dynamics Kepler's 2nd law formal solution LN 4.1.1 HF 4.1-4.4 |
Nov 23 Thanksgiving holiday |
Nov 24 |
| Nov 28 central force motion 1/r2 central force solutions scattering and cross sections LN 4.1.2 HF 4.5-4.7 |
Nov 30 Review for final Slides |
Dec 1 Problem Set 7 due solutions posted v. 3 posted, 1/15 Final exam posted Final exam due Dec 8 solutions posted v. 2 posted, 1/3 |
| Winter, 2007 |
||
| Jan 2 No class |
Jan 4 mathematical description of rotations infinitesimal and finite rotation matrices tensors Lie algebras and groups LN 5.1 HF 7.1-7.4 (Th 1.2-1.8) |
Jan 5 Problem Set 8 posted v. 3 posted 1/12 |
| Jan 9 rotating coordinate systems obtaining an effective eqn of motion LN 5.2.1-5.2.2 HF 7.5-7.8 (Th 10) |
Jan 11 rotating coordinate systems applications dynamics of rigid bodies mathematical description of rigid body motion LN 5.2.3, 5.3.1 HF 7.9, 8.1-8.3, 8.7-8.8 (Th 11.1-11.8) |
Jan 12 Problem Set 8 due solutions posted Problem Set 9 posted v. 3 posted 1/18 |
| Jan 16 dynamics of rigid bodies dynamics of torque-free rigid bodies LN 5.3.2 HF 8.4-8.6 (Th 11.9-11.10) |
Jan 18 dynamics or rigid bodies dynamics of rigid bodies with torque LN 5.3.3 HF 8.10 (Th 11.11) |
Jan 19 Problem Set 9 due solutions posted Problem Set 10 posted |
| Jan 23 special relativity basic postulates transformation laws LN 6.1.1-6.1.2 HF 12.5-12.8, read only the first two subsections of 12.6 |
Jan 25 special relativity physical implications Lagrangians and Hamiltonians in SR LN 6.1.4-6.1.5 HF 12.9-12.12, 12.14 |
Jan 26 Problem Set 10 due solutions posted Problem Set 11 posted |
| Jan 30 special relativity ctd mathematical description LN 6.1.3 classical field theory continuous string example generalized calculus of variation EOM for nonrelativistic fields |
Feb 1 classical field theory Noether's theorem Hamiltonian mechanics gauge transformations |
Feb 2 Problem Set 11 due solutions posted Midterm posted Midterm due Feb 9 solutions posted |
Exams
Exam Parameters: All exams will
be 4 hours, to be done in one sitting, but with a total of 30 minutes
of break time allowed. Policies on what materials you may use are
given above.
Midterm, Fall term: This exam will cover material through Oct 19 and in addition the material on Oct 24 on using Lagrange multipliers to implement constraints in variational dynamics. Topics that Ph196 students will be responsible for but will not be required for Ph106 students:
Exam (including instructions, 3 pages): Don't download this until you are ready to take the exam.
Solutions (typo on Problem 4 soln corrected, 2006/11/07)
Comments: this exam was too easy by about 10 points. On problem 4, one could miss subtle parts of the problem with losing a lot of points.
Final, Fall term: This exam will cover all material from the term. In addition to the above, the 196-only topics are:
Exam (including instructions, 4 pages): Don't download this until you are ready to take the exam.
Solutions (Version 2 posted, 2007/01/03).
Comments: This median score was 62 with rms 26. I was hoping for a median of about 70. This was primarily the fault of problem 4, for which the median score was 5/20 points; if it had been 13/20 or 15/20, the median would have come out in the right place. Specific points:
Exam (including instructions, 3 pages): Don't download this until you are ready to take the exam.
Solutions (Version 2 posted, 2007/02/16 to reflect other possible reading of Problem 3).
Comments: This median score was 52, mean 48, rms 26. A bit of a bloodbath. Again, I was hoping for a median of about 70. This was primarily the fault of problem 3, for which the median score was 4/20 points.
Midterm, Fall term: This exam will cover material through Oct 19 and in addition the material on Oct 24 on using Lagrange multipliers to implement constraints in variational dynamics. Topics that Ph196 students will be responsible for but will not be required for Ph106 students:
- virtual work and generalized forces
- derivation of Euler-Lagrange equations via virtual work
- nonholonomic constraints
- Lagrangians for nonconservative forces
- Dealing with nonholonomic constraints using Lagrange multiplier methods
Exam (including instructions, 3 pages): Don't download this until you are ready to take the exam.
Solutions (typo on Problem 4 soln corrected, 2006/11/07)
Comments: this exam was too easy by about 10 points. On problem 4, one could miss subtle parts of the problem with losing a lot of points.
Final, Fall term: This exam will cover all material from the term. In addition to the above, the 196-only topics are:
- Legendre transformations
- canonical transformations and generating functions
- symplectic notation, Poisson brackets, action-angle variables, and Hamilton-Jacobi theory
- mathematical structure of coupled oscillations
Exam (including instructions, 4 pages): Don't download this until you are ready to take the exam.
Solutions (Version 2 posted, 2007/01/03).
Comments: This median score was 62 with rms 26. I was hoping for a median of about 70. This was primarily the fault of problem 4, for which the median score was 5/20 points; if it had been 13/20 or 15/20, the median would have come out in the right place. Specific points:
- Problem 1: the median score was 15/20 points. That's
probably about right -- looks like most people got most of the problem
right, missing a few points here and there due to mistakes.
- Problem 2: The "quickie" problems did not really serve their
purpose of being very easy: the median score was 15/20 points, no
better than problem 1. I'm sure many of you will be surprised at
how straightforward these are when you see the solutions.
- Problem 3: This turned out to be the easy one. So you know
coupled oscillations well -- I'm glad to see that.
- Problem 4: It looks like you either got it or you didn't. I
should have given a hint to make it clear what needed to be done --
find the particles with impact parameter that bring them closer to the
planet than its radius R -- which would have pushed the median up a lot.
- Problem 5: (a) and (c) seemed to cause the most trouble, while (b) was more doable. This is unfortunate but not surprising, as (a) and (c) required almost no calculation, just physics, while in (b) one could just rely on the procedure for solving an inhomogeneous differential equation and get almost all the points.
- Lie groups
- Mathematics of special relativity
- Classical field theory
Exam (including instructions, 3 pages): Don't download this until you are ready to take the exam.
Solutions (Version 2 posted, 2007/02/16 to reflect other possible reading of Problem 3).
Comments: This median score was 52, mean 48, rms 26. A bit of a bloodbath. Again, I was hoping for a median of about 70. This was primarily the fault of problem 3, for which the median score was 4/20 points.
- Problem 1: median score = 14, reasonable.
- Problem 2: median score = 15, reasonable. I'm glad that you
understand rotating systems.
- Problem 3: median score = 4. This was supposed to be easy
-- you'll probably be kicking yourself when you see the solution.
I'd appreciate hearing why it was difficult. I gather that some
of the low grades may have been because one can read the problem in
such a way as to infer the opposite velocity as intended. If so,
you should get full credit if you did the problem correctly under that
interpretation. A solution for that reading of the problem has
been added. I also have the impression
is that there are some somewhat correct solutions that were not given
enough credit. If you feel that your solution is partially or
wholly correct and did not receive enough credit, contact Andrey.
If you can't arrive at a satisfactory
solution with Andrey, contact me.
- Problem 4: median score = 10. This was supposed to be
difficult conceptually, looks like it was.
- Problem 5: median score = 10. This was largely a matter of
Taylor expanding the effective potential. Not sure what else to
say.
Practice Problems
Use these problems to check your
understanding and develop your physical intuition. Solution sets
are available by email request.
2004-2005 Problem Sets:
2004-2005 Problem Sets:
- 2004-2005 Problem Set 1: single-particle Newtonian mechanics and gravitation
- 2004-2005
Problem Set 2: Newtonian dynamics of systems of particles
- 2004-2005
Problem Set 3: virtual work, Lagrangian mechanics
- 2004-2005
Problem Set 4: variational dynamics, with and without constraints
- 2004-2005
Problem Set 5: basic and advanced topics in Hamiltonian dynamics
- 2004-2005
Problem Set 6: simple harmonic oscillator
- 2004-2005
Problem Set 7: coupled oscillations, waves, continuous systems
- 2004-2005
Problem Set 8: central forces and scattering
- 2004-2005
Problem Set 9 : rotating coordinate systems
- 2004-2005
Problem Set 10: dynamics of rigid bodies
- 2004-2005
Problem Set 11: special relativity
- 2005-2006 Problem Set 1: single-particle Newtonian mechanics and gravitation
- 2005-2006
Problem Set 2: Newtonian dynamics of systems of particles
- 2005-2006
Problem Set 3: Lagrangian mechanics
- 2005-2006
Problem Set 4: symmetry transformations, variational mechanics
- 2005-2006
Problem Set 5: constraints in Lagrangian mechanics, basic and
advanced topics in Hamiltonian dynamics
- 2005-2006
Problem Set 6: Liouville's theorem, Poisson brackets, H-J eqn,
simple harmonic oscillator
- 2005-2006
Problem Set 7: coupled oscillations, waves, continuous systems
- 2005-2006 Problem Set 8: special relativity
- 2005-2006
Problem Set 9 : central forces and scattering
- 2005-2006
Problem Set 10: rotating coordinate systems
- 2005-2006 Problem Set 11: dynamics of rigid bodies
- 2004 Fall Midterm: Material
through variational dynamics
- 2004 Fall Final: All material
through waves and continuous systems
- 2005 Winter Midterm: Central forces, rotating systems, rigid body motion, making use of some material from Fall 2004.
- 2005 Fall Midterm: Material
through variational dynamics
- 2005 Fall Final: All material
through waves and continuous systems
- 2006 Winter Midterm: Special relativity, central forces, rotating systems, rigid body motion, making use of some material from Fall 2004.
Comment on Working in Groups:
It is in general a good thing to work
with other students while reading and doing problem sets. You get
to hear different perspectives on the material and frequently your
peers can help you get past obstacles to understanding.
However, you must use group work carefully. If you rely on your colleagues too much, or take a very long time to do the homework sets, you will do poorly in the fixed-time, independent exam environment. Empirically, we observe that students with good exam scores tend to also have done well on homework, but that good homework scores do not predict good exam scores. Exam scores correlate from exam to exam, even on largely independent material. For example, scores from 2004-2005 Ph106ab:

Notice, in particular, the midterm-final correlation for Ph106b, which is remarkable because the exams covered totally disjoint material (mechanics vs. E&M) and were written by two different instructors.
To avoid suffering from this problem, I have two suggestions:
However, you must use group work carefully. If you rely on your colleagues too much, or take a very long time to do the homework sets, you will do poorly in the fixed-time, independent exam environment. Empirically, we observe that students with good exam scores tend to also have done well on homework, but that good homework scores do not predict good exam scores. Exam scores correlate from exam to exam, even on largely independent material. For example, scores from 2004-2005 Ph106ab:

Notice, in particular, the midterm-final correlation for Ph106b, which is remarkable because the exams covered totally disjoint material (mechanics vs. E&M) and were written by two different instructors.
To avoid suffering from this problem, I have two suggestions:
- Talk to your peers, in particular peers outside of your usual
workgroup, to find out how long they are spending on problem
sets. If you find you are spending much more time, figure out
why! Do you need to spend more time understanding the material
before diving in to problem sets? Do you jump to an incorrect
solution method too quickly? Are you getting bogged down in
algebra? Consult me or the TAs too.
- While working in groups can be helpful, you have to be careful to
remain sufficiently independent that you can solve problems on your
own! My suggestion is to go over the material and examples in
groups, but try to work the problems by yourself, using help from
others as a last resort. If you find yourself helping one of your
peers, don't just explain how to do the problem; try to help him find
his way to the solution himself.
This is not just an arbitrary classroom
exercise. In research, one is always under schedule pressure --
because one only has a fixed number of nights at an observatory,
because there are funding deadlines, because there are competing groups
doing similar work. It is critical to learn how to cut through
irrelevant or unimportant information and get to results in a timely
fashion.
Announcements Archive
- 2007/02/16
- Conversations with some of you have made clear how Problem 3
could be read differently than intended. A solution corresponding
to that reading has been added. Again, contact Andrey for
regrading if you think you deserve more credit for the problem.
- 2007/02/13
- PS11 and midterms graded and available for pickup. See discussion of midterm below. Note: I am not confident that enough partial credit was assigned in Problem 3. See below. A good opportunity to discuss your solution with Andrey will be office hours on Wed 2/14. Contact him if you would like him to start office hours early (8 pm) for this.
- 2007/02/09
- Midterm solutions posted.
- We have a PS11 with no name on it. It is 2 pages long and
has only Problems 1 and 3 done. It will be pinned to the board
above the in-box. If it is yours, please put your name on it and
place it in the in-box.
- 2007/02/07
- Unless there is popular
demand, office hours on Thursday night will be canceled.
- 2007/02/06
- PS10 available for pickup.
- 2007/02/05
- Midterm exam posted. Due
Feb 9, 5 pm.
- 2007/02/04
- PS11 solutions posted. Figure for Problem 5c and soln for Problem 7 will be posted on Monday.
- Update listing of topics to be covered on midterm, below. Midterm is due Feb 9, not Feb 10 (old calendar error).
- Midterm will be posted Monday morning.
- 2007/02/01
- PS9 is available for pickup. We will have PS10 available
on Feb 6. You should keep a copy of your PS11, we will not have
them graded before the midterm is due.
- 2007/01/30
- Syllabus updated for today's and Thursday's lectures.
Sorry for the late notice! All
topics covered this week are optional! (since I won't be
able to give you homework on them). Notes will be handed out in
class and posted.
- 2007/01/28
- PS11 posted.
- PS8 available for pickup (actually, it was available Thursday
night, I forgot to post a notice.)
- 2007/01/27
- PS10 solutions posted. Solution for Problem 6 not written
yet. H&F did have errors in Problem 3.
- 2007/01/24
- Problem 3: There are some indications that H&F is missing a
factor of (1/2) in the second term in E',
and also that its numerical results in (b) are not correct. We're
checking it, so don't worry about it yet if your result doesn't match
H&F. Further information to be posted here.
- 2007/01/22
- For Problem 1, it is possible to avoid needing a table of
integrals or Mathematica if you know the right technique for doing the
integrals.
- 2007/01/21
- PS9 solutions posted.
- 2007/01/20
- PS10 posted.
- 2007/01/19
- A few more typos found in Problem 5 thanks to questions in
office hours -- a couple signs and numerical prefactors. See
updated version of problem set. Given the late date that these
errors were found, we will be lenient about any incorrect answers that
result from them.
- 2007/01/18
- Typo in lecture notes that may affect your ability to do
Problem 2. On p. 276 of the 9/25 version of the notes, or p. 285
of the most recent version, we state
This is inconsistent with the generic formula for the inertia tensor, there should be a minus sign in front of the right side. This really ought not to make any difference in your results for the problem for reasons that hopefully will become apparent when you do the problem.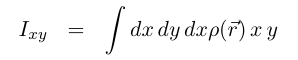
- 2007/01/17
- Version 2 of PS9 posted -- correction to kinetic energy in
Problem 5, more hints given.
- 2007/01/15
- Updated lecture notes errata with aforementioned corrections posted below.
- 2007/01/13
- PS8 solutions posted
- PS9 posted. Note:
I need to correct a couple typos in Section 5.2.3 of the lecture notes
to avoid confusion on Problem 3. Look for those corrections later
this week.
- 2007/01/12
- 11:30 am: Problem 6 (196b
only!) is written in a misleading way. Replace

with

The full problem set below has been updated. Given the late notice on this, you may turn in this problem up to 1 week late at full credit.
- Office hours last night indicated there was significant
confusion about how to deal with expressions like
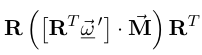 and
and 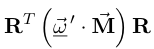 that arise in
problem 5; in particular, in the first expression, why is it that R
cannot just be canceled with the first RT? How to evaluate such
expressions is discussed in the section Acceleration and Fictitious Forces
in Section 5.2.1 of the notes as well as earlier in Examples of Tensors in Section
5.1.4. When any confusion arises, you should just revert to
tensor index notation as is used in Section 5.1.4.
that arise in
problem 5; in particular, in the first expression, why is it that R
cannot just be canceled with the first RT? How to evaluate such
expressions is discussed in the section Acceleration and Fictitious Forces
in Section 5.2.1 of the notes as well as earlier in Examples of Tensors in Section
5.1.4. When any confusion arises, you should just revert to
tensor index notation as is used in Section 5.1.4.
- 2007/01/11
- Clarifications on PS8 -- see v. 2 posting below.
- 1) The second half of the question is not very clear. See revised version.
- 3) You should assume the orthogonal matrices are real. All rotation matrices we will consider are real.
- 6) "given by the angle between the two axes of rotation" is
misleading. See revised version.
- 2007/01/10
- I checked with Prof. Cross about continuing various policies into the second half of the term -- everything will continue as-is. Specifically:
- Ph196b is being offered. I have requested the registrar make it available -- give them a day or so before you try to switch into it.
- One free extension policy will continue, but you get one over the entire term, not one from each of us.
- 50% credit for late HW and split of on-time/late portions of HW will continue.
- Open-book exam policy will continue.
- 2007/01/06
- Problem Set 8 posted.
- 2007/01/03
- Updated final exam solutions posted -- simpler solution to (1c), more explicit solution for (2), and better solution for (7).
- Updated solution for Problem Set 7 #5 (the relativistic precession problem) posted. The expansion about the circular orbit is a very good example of a Taylor expansion in classical mechanics, I strongly suggest you read it.
- Lecture notes errata and corrected lecture notes posted below.
- 2006/12/15
- All PS7's and final exams received have been graded and grades have been submitted. They are available in the out-boxes for pickup. Check the anonymous grade list to make sure we made no mistakes.
- We still have a little bit of cleanup on the final exam and PS7
solutions to do. Check back on Monday (if you're really that
interested...).
- 2006/12/12
- Final exams graded and ready for pickup. See below for solutions and some
discussion.
- Grade histograms and anonymous grades posted below.
- Note: Due to my misreading of an email from the TAs, many of your on-time PS6s were not available for pickup for use in studying for the exam. If anyone honestly feels that this put him/her at a disadvantage on the exam, I am willing to consider grade adjustments. Send me email with an explanation.
- Aforementioned PS6's available for pickup.
- Many PS7's were turned in at the end of last week, making it difficult for the TAs to get them and the exams all graded over the past weekend. I can't assign final grades until they are done, so final grades will be delayed.
- 2006/12/04
- On-time PS6's available for pickup.
- Final exam posted (finally!)
- Another small typo found in PS6 solutions, see updated copy below.
- 2006/12/03
- If you have taken an extension on PS7: please try to get these in before
Dec 8. We already have to grade all the exams over the weekend of
Dec 9/10 and get grades in by Dec 13.
- PS7 solutions posted.
- Corrections to solutions for PS5 and PS6. See updated solutions.
- Final exam available later today.
- 2006/12/02
- Slides from review for final posted below.
- PS6 will be returned on Monday, Dec 4. Apologies for the delay, hopefully this still allows plenty of time to review it for the final.
- PS7 solutions to be posted on Sunday.
- Final exam to be posted on Sunday.
- Thursday Dec 7 office hours: probably too late to be of any
use? I will cancel unless there is popular demand to keep
them. Let me know if you have any preference for one of the
following options. If there is no response, I will do option (1):
- Daytime office hours during normal class time slot on Dec 7.
- I take over Wednesday night office hours on Dec 6.
- Daytime office hours at some other time during the week. Tuesday is not available, Wednesday afternoon could work.
- 2006/11/30
- NOTE ON PS7: There is a typo
in the notes for the Rutherford cross section in Section 4.3.3 of the
lecture notes. The differential cross section should be
proportional to 1/sin^4 (theta_star/2), not 1/sin^2
(theta_star/2). You need this correction to do Problem 6
correctly.
- 2006/11/29
- PS5 available for pickup, PS6 available later this week. Updated grade sheet to be posted soon.
- Course evaluations will be
handed out on Thursday, please attend to fill one out.
- 2006/11/28
- Remember to keep a xerox copy of your PS7: they will not be returned before the final exam is due.
- Astrophysics majors really ought to try PS7 #8: it's a very
common phenomenon in astrophysics.
- 2006/11/27
- Clarifications on PS7, #5: The energy E is the nonrelativistic
kinetic + potential energy. The unperturbed potential V(r) should
be assumed to be Keplerian, V(r) = - G \mu M / r.
- 2006/11/21
- Midterm and old problem set grading corrections done -- see the
outboxes and the anonymous grade
sheet.
- Rather belated posting of Problem Set 7.
- PS06 solutions posted.
- Problem Set 6 will be returned next week.
- No office hours this week.
- 2006/11/16
- Clarifications added to Problem Set 6: see version 2 below.
- 2006/11/12
- Reminder: No lecture
Tuesday Nov 13
- 2006/11/11
- PS5 solutions posted.
- 2006/11/10
- PS6 posted.
- Misprints in PS4 solutions
corrected, see below for
updated version
(8:30 pm: now it's really there!)
- 2006/11/09
- Some changes have been made to the end-of-term syllabus: we will do central forces this term and save relativity for next term. The latter is easier to do after we have discussed rotations.
- Midterm grade corrections have been done and exams are
available for pickup this morning. Still working on some problem
set grade corrections.
- 2006/11/08
- Note on PS5 #2: You may
assume that p_z >> p_x and p_y and thus that it is unchanged to
good approximation.
- This week's Thursday night office hours will be held by Andrey
in the usual SFL room.
- 2006/11/07
- Midterm exams available for pickup.
- Grade histograms and anonymous grade sheet posted.
- Minor typo in Midterm Problem 4 solution corrected, other typos have been found and will be corrected.
- 2006/11/05
- PS5 posted (8 am, discard any versions from earlier this
morning)
- 2006/11/04
- Midterm solutions posted. We should have them graded and
ready for pickup on Tuesday.
- 2006/11/01
- PS3 available for pickup
- 2006/10/30
- PS4 solns posted
- Midterm posted
- Lecture notes errata later tonight...
- 2006/10/28
- I've fallen ill and so will be delayed in posting the midterm,
PS4 solutions, and typo corrections to the lecture notes. I am
certain all these will be available on Monday.
- Since we have covered Lagrange multipliers in PS4, they will be covered on the midterm. See below for details on what will be on the midterm, reference policies, time allowed, etc.
- We will have standard office hours this coming week.
- 2006/10/25
- Minor corrections to PS4 posted. See updated version (#2) below.
- Keep a xerox copy of your PS4. They will not be graded and returned before you have to do the midterm.
- Thanks for all the lecture note typo corrections -- keep them
coming. I will post the corrections before the midterm is due.
- 2006/10/22
- Updated syllabus posted -- speeding up a bit to eliminate the
rescheduled lecture
- 2006/10/21
- PS3 solutions posted
- PS4 posted
- 2006/10/19
- A couple clarifications on PS3 following office hours:
- Problem 2: By "stable" and "unstable", we mean in the sense
of Section 1.1.3 of the lecture notes. You must prove your claims
of stability or instability mathematically.
- Problem 3: You may assume the simplest possible situation: the pendulum is moving in a plane parallel to one of the walls of the box, that the box does not move in the perpendicular plane nor does it spin (these should be obvious from the first statement).
- Problem 4: In the clarification for part (b), where we say to find \dot{x}(t) in terms of x, f(x), and E, it may include the derivatives f' and f''.
- PS1 and PS2 available for pickup outside my office.
- 2006/10/18
- PS3 note: on problem 6 (196a only), don't be surprised if you
get sign flips or exchange the sines and cosines: the angle convention
for the problem is not clear. In particular, H&F uses a
different angle convention than the problem, which came from Goldstein.
- 2006/10/15
- PS3 v. 2 posted -- correction to problem 4, Eqn 1.95 in HF is correct.
- PS2 solutions posted.
- 2006/10/14
- PS3 posted
- Message from Dean Hall regarding how to register for 196a yet
still allow the option of dropping down to 106a later -- posted below.
- 2006/10/07
- PS1 solutions posted (correction to problem 5 posted, v. 2)
- PS2 posted
- 2006/10/03
- Location of Weds night office hours changed -- 231 SFL.
- 2006/10/01
- Type in PS1 #5 found. Corrected version (v. 2) posted.
- 2006/09/30
- PS1 posted.
- 2006/09/28
- Lecture notes are available in the bookstore.
- 2006/09/25
- Updated page for 06-07.